Adversarial Autoencoders for Molecular generation
This blog states about dome pros and cons of Variational Autoencoder. It also consequently introduces a new method called Adverserial Autoencoders for better generation of molecules.
In my earlier two blogs, you have seen how vae helps to create SMILES(text generation) of a similar kind.Now, before coming into the Adversarial Autoencoder lets see some drawbacks of Variational autoencoder(VAE). There are many models which work similarly to the VAE. They also help us to understand the similar input generation. But there is a slight difference between VAE and others and both are known to work on same things. Why we use other models instead of VAE for similar input generation.
Today we will see the drawbacks of VAE and how Generative adversarial network and Adversarial autoencoder is better than Variational autoencoder.
The assumption we made in VAE is that we used another distribution also known as Gaussian distribution and imposed this distribution to our latent vector distribution. We have done so as we don’t know the input data distribution and for doing this, we use KL-divergence to make the similar distribution.
To know more about VAE and KL-divergence, please refer to my previous blogs
We take assumption while using KL-divergence that the two distribution will overlap each other. But what if they don’t overlap each other and that is where the confusion lies.
If this does not happen then our KL-divergence gives the $\infty$ value giving us some weird results and that is non-trackable. Let’s understand that by a simple example
Let’s say $Q(x)$ and $P(x)$ is the probability distribution function and we want to measure the KL-divergence of these distributions.
And we have values of
and then
To overcome this drawback, we use Jensen-Shannon Divergence(JSD) divergence and Wasserstein divergence.
JSD divergence: It is a method to measure the similarity between two probability distribution function.
It is same as the KL-divergence method but with better results.
JSD-divergence = $JSD(P||Q) = \frac{1}{2}[KL(P||M) + KL(Q||M)]$
Where $M = (P + Q)/2$
Advantange of JSD over KL-divergence is its symmetric nature means $JSD(P||Q) = JSD(Q||P)$
Now lets again see the above example we measure the JSD divergence between two probability function $P(x)$ and $Q(x)$
And the advantage of GAN over VAE is that it uses JSD divergence instead of KL-divergence.
Now there is one problem in JSD divergence and this is when the two distribution functions far from each other. Then it only gives constant value log2 and when we take the gradient of JSD divergence after some point it provides 0 value.
But this is not great news for the model. So now we want a method which will help us to measure gradient. At the same time, it also helps to measure the similarity between two probability distribution function.
To overcome this, we use Wasserstein distance, which is also called earth mover distance.
I am not going much deep in this concept as the blog might become huge. In reference, I will provide you with a link if we want to know the concepts of Wasserstein distance
Wasserstein distance.
When we use Wasserstein distance in GAN, we called GAN as WGAN.
Adversarial Autoencoder
An adversarial autoencoder is a type Generative adversarial network in which we have an autoencoder and a discriminator.
In Autoencoder part we have Encoder, Decoder and Latent vector. Please click on the respective link if you want to know about these terms.
Auto-encoder try to give output as same as the input but we want to generate a similar input. We don’t want the same input and thus we take a sample from latent vector and put into the decoder to give similar output. But the problem lies in the fact that we are unaware of the distribution of latent vector.
So we take a random distribution we are aware of and try to put that distribution into latent distribution. You should also remember to impose this distribution into the latent distribution we use JSD divergence because we see JSD is better than KL-divergence.
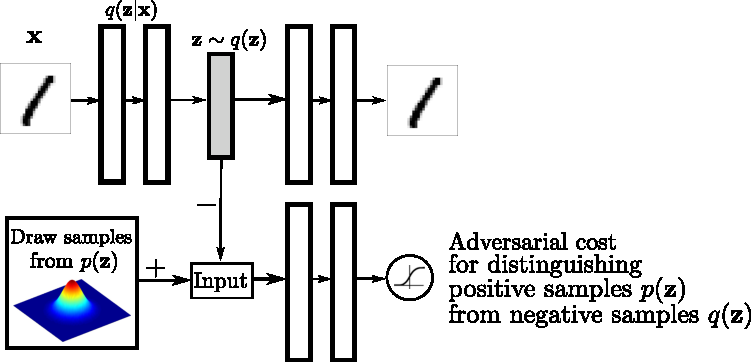
You can see from the above image that x is our real distribution and $q(z|x)$ is our encoder. $z\sim q(z)$ is a sample taken from q(z), and from this distribution, we make a similar distribution.
Proposition of AAE
To make adversarial autoencoder, we first train our autoencoder to make the same images. Why we do this before, you will understand it later. After the autoencoder part which is trained now, we will train our generator part. Now what we do is, we take a sample from our dataset, pass it through the encoder. Now we take a sample and give it to the discriminator and make them labels as 0.and we took a sample from real data p(z) and pass it to the discriminator and make them labels as1.
Remember one thing, here discriminator act as a classifier. It only classifies data which is coming from the dataset and real distribution and the discriminator work is to differentiate this. We trained the discriminator until the discriminator was unable to differentiate between the real dataset and fake. When this happens we understand that now our $q(z)$ is somewhat similar to the $p(z)$ and now we take a sample and pass through the decoder to make similar input.
Loss Function of AAE
Reconstruction Loss: This loss tries to minimize the error between real image and generated image
Regularization Loss: $min_E max_D {E_{z \sim p_z(z)}[logD(z)] + E_{x \sim p_d(x)}[log(1-D(E(x))]}$.
To understand the regularization Loss first understand the terms
$D(z)$ is sample taken from distribution of real sample means taken from p(z).
$p_{d(x)}$ is taken data from dataset.
$D(E(x))$ is data coming from encoder and then feed into the discriminator.
To understand why in regularization loss minmax function is there, please visit Loss this video explains the concept easily.
Note
Here encoder plays two crucial roles
- Encoder when we use an autoencoder
- Generator when we use GAN training means when we use discriminator.
Let’s see the code of AAE in pytorch.In this code, we see text generation by using SMILES(molecular generation)
I used pycharm; I suggest you to use google collab for this code and please reduce the size of the data as real data needs a huge computation. To see the full code please visit this Github page.
Import dataset and data-preprocessing:
We use the same dataset as we use in VAE and also same vocabulary
The data preprocessing part is same in VAE and AAE. In the previous link I have already explained about data preprocessing.
Model:
In the model section, we make 3 class that I already told you encoder, decoder and discriminator.
We feed our vocabulary first to an encoder and this encoder tries to encode the input data and make a small vector which representation our whole input data. Now the decoder takes input from this small dimension latent vector and converts it back into our original data.
here we use RNN with Adversarial Autoencoder as for similar text generation
class encoder(nn.Module):
def __init__(self, vocab, emb_dim, hidden_dim, latent_dim):
super(encoder, self).__init__()
self.hidden_dim = hidden_dim
self.latent_dim = latent_dim
self.emb_dim = emb_dim
self.vocab = vocab
self.embeddings_layer = nn.Embedding(len(vocab), emb_dim, padding_idx=c2i['<pad>'])
self.rnn = nn.LSTM(emb_dim, hidden_dim)
self.fc = nn.Linear(hidden_dim, latent_dim)
self.relu = nn.ReLU()
nn.Drop = nn.Dropout(p=0.25)
def forward(self, x, lengths):
batch_size = x.shape[0]
x = self.embeddings_layer(x)
x = pack_padded_sequence(x, lengths, batch_first=True)
output, (_, x) = self.rnn(x)
x = x.permute(1, 2, 0).view(batch_size, -1)
x = self.fc(x)
state = self.relu(x)
return state
......
to see decoder and discriminator code please visit the above-given link
Training:
To train the model first, we have to divide the model into two parts first is autoencoder which is encoder and decoder. By doing this we can easily regenerate our data back this training we call as pre-train.
After pretraining, we train our generative part so now we use encoder and discriminator in this training when data comes from the real dataset, i.e. from encoder we make them label 0 and when data comes from real distribution we make them label 1. And feed into the discriminator, it tries to discriminate, but we train them until our discriminator does not differentiate between encoder input and real distribution input.
def pretrain(model, train_loader):
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(list(model.encoder.parameters()) + list(model.decoder.parameters()), lr=0.001)
model.zero_grad()
for epoch in range(4):
if optimizer is None:
model.train()
else:
model.eval()
for i, (encoder_inputs, decoder_inputs, decoder_targets) in enumerate(train_loader):
encoder_inputs = (data.to(device) for data in encoder_inputs)
decoder_inputs = (data.to(device) for data in decoder_inputs)
decoder_targets = (data.to(device) for data in decoder_targets)
latent_code = model.encoder(*encoder_inputs)
decoder_output, decoder_output_lengths, states = model.decoder(*decoder_inputs, latent_code,
is_latent_state=True)
decoder_outputs = torch.cat([t[:l] for t, l in zip(decoder_output, decoder_output_lengths)], dim=0)
decoder_targets = torch.cat([t[:l] for t, l in zip(*decoder_targets)], dim=0)
loss = criterion(decoder_outputs, decoder_targets)
if optimizer is not None:
optimizer.zero_grad()
loss.backward()
optimizer.step()
..
to see the full training code visit click on the above link
Sampling:
After training is done, our model IS completed. Now our real distribution will be imposed well on our latent distribution.
Now we take samples from our latent distribution and feed into the decoder generate similar data as of input data.
def sample(model,n_batch, max_len=100):
with torch.no_grad():
samples = []
lengths = torch.zeros(n_batch, dtype=torch.long, device=device)
state = sample_latent(n_batch)
prevs = torch.empty(n_batch, 1, dtype=torch.long, device=device).fill_(c2i["<bos>"])
one_lens = torch.ones(n_batch, dtype=torch.long, device=device)
is_end = torch.zeros(n_batch, dtype=torch.uint8, device=device)
for i in range(max_len):
logits, _, state = model.decoder(prevs, one_lens, state, i == 0)
currents = torch.argmax(logits, dim=-1)
is_end[currents.view(-1) == c2i["<eos>"]] = 1
if is_end.sum() == max_len:
break
currents[is_end, :] = c2i["<pad>"]
samples.append(currents)
lengths[~is_end] += 1
prevs = currents
if len(samples):
samples = torch.cat(samples, dim=-1)
samples = [tensor2string(t[:l]) for t, l in zip(samples, lengths)]
else:
samples = ['' for _ in range(n_batch)]
return samples
This code is hard to understand but once you have a good grasp, you will get the whole concept
I hope you like it.
If you have any doubts and if you want a certain kind of content, please visit us. Would you like to see more on this blog? Let us know in the comments section.
Till then keep learning :)
Refrences
alhad kumar video explanation and git hub code moses